特征值、特征向量和奇异值分解

2017.09.15
SF-Zhou

最近准备各种笔试，顺便复习了一下矩阵的相关知识。找到了一份非常棒的学习视频：线性代数的本质。这份学习材料是 3Blue1Brown 制作的，视频中会使用几何的方式揭示矩阵操作的本质。在 YouTube 和 Bilibili 上有官方提供的视频，都有中文字幕。视频中提到的特征值、特征向量还有基变换，都给了关于矩阵的全新的理解。所以在这里总结一下。

一、基与向量

一开始的时候，世界是虚无的。所以基 i^\hat i 和 j^\hat j 被定义了，如图 (a) 所示。

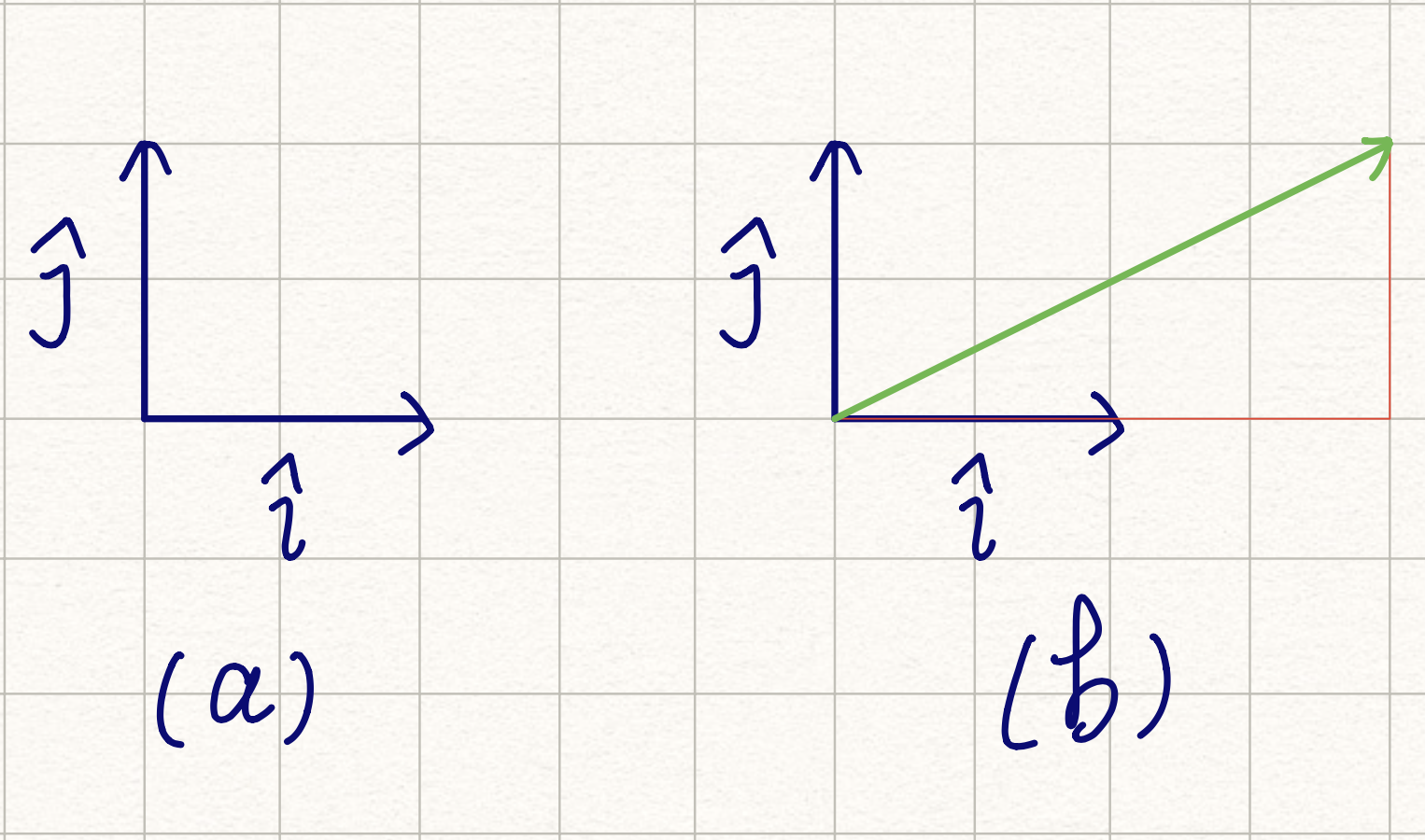
有了基之后，空间里的向量都可以轻松地被表示出来。(b) 图中绿色的向量可以表示为 (2i^,j^)(2 \hat i, \hat j)。

二、矩阵和变换

想象一下，现在把基 i^\hat i 和 j^\hat j 拉到 i^′\hat i' 和 j^′\hat j' 的位置，如图 (c) 所示。图 (b) 中绿色的向量也同时被拉伸了。

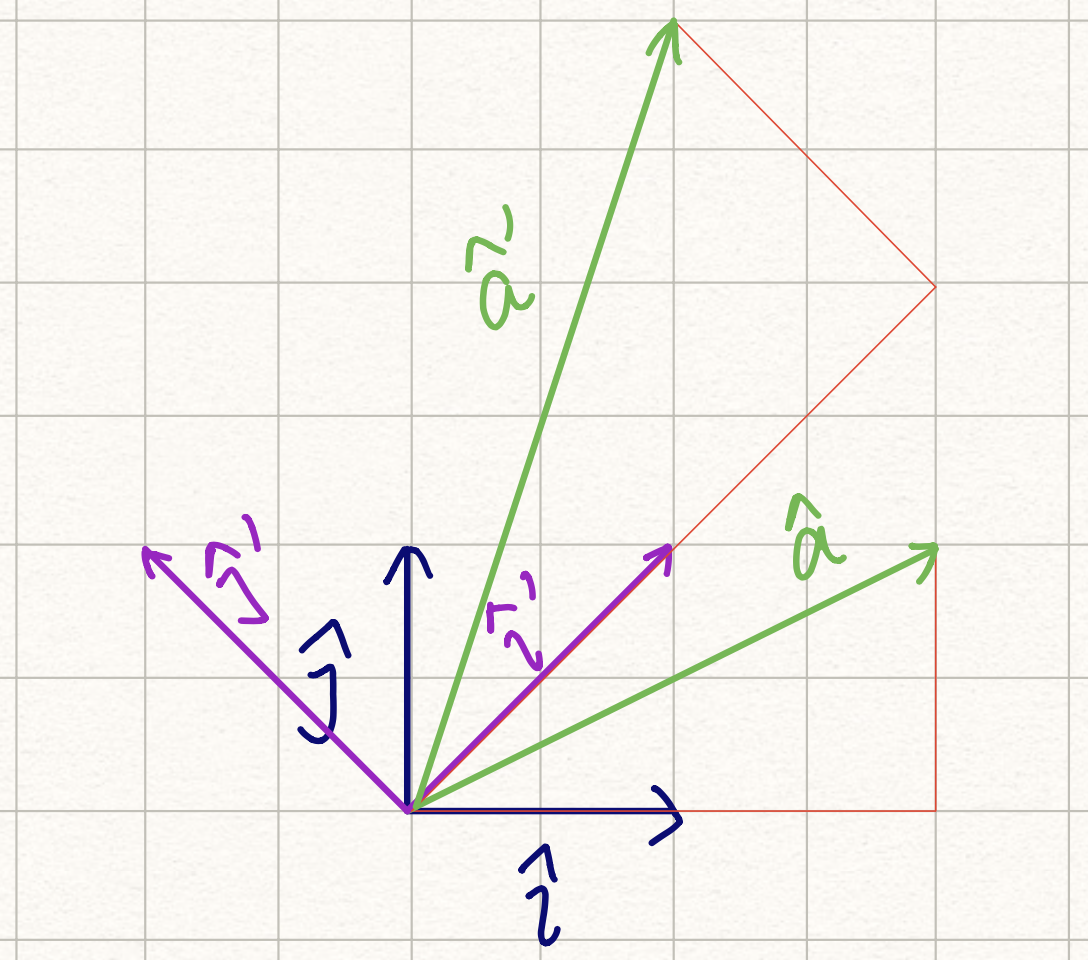
拉伸后的向量 a^′\hat a'，使用新的基表示，仍然是 (2i^′,j^′)(2 \hat i', \hat j')。同时，i^′\hat i' 和 j^′\hat j' 可以使用原先的基表示：

i^′=i^+j^j^′=−i^+j^ \begin {aligned} \hat i' &= \hat i + \hat j \\ \hat j' &= -\hat i + \hat j \end {aligned}

也就是 i^′=(i^,j^)\hat i' = (\hat i, \hat j)，j^′=(−i^,j^)\hat j' = (-\hat i, \hat j)。所以：

a^′=2i^′+j^′=i^+3j^ \hat a' = 2 \hat i' + \hat j' = \hat i + 3 \hat j

简单来说，变换后的向量 a^′\hat a'，使用原先的基表示，为 (i^,3j^)(\hat i, 3 \hat j)。

总结一下，变换后，空间中的向量与新的基的系数关系没有发生改变。而基本身改变了，向量在原来基中的表示发生对应的变化。这种变化，就是两个基变换的叠加。这种变换，就可以表示为矩阵：

[i^/i^′−i^/j^′j^/i^′j^/j^′]a^′=[i^/i^′−i^/j^′j^/i^′j^/j^′][2i^′j^′]=[i^3j^] \begin{bmatrix} \hat i / \hat i' & -\hat i / \hat j' \\ \hat j / \hat i' & \hat j / \hat j' \end{bmatrix} \hat a' = \begin{bmatrix} \hat i / \hat i' & -\hat i / \hat j' \\ \hat j / \hat i' & \hat j / \hat j' \end{bmatrix} \begin{bmatrix} 2 \hat i'\\ \hat j' \end{bmatrix} = \begin{bmatrix} \hat i\\ 3\hat j \end{bmatrix}

简化一下，变换可以记录为：[1−111]\begin{bmatrix}1 & -1 \\ 1 & 1\end{bmatrix}。而变换可以从两个角度看：

  1. 可以计算变换后，原先空间中的向量变换后到位置；
  2. 可以计算在新的基下，一个向量映射到原先基中的位置。

三、基变换

在基 (i^′,j^′)(\hat i', \hat j') 中，向量 a^′\hat a' 可以通过乘上变换矩阵，得到在基 (i^,j^)(\hat i, \hat j) 中的表示：

[1−111][21]=[13] \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ 3 \end{bmatrix}

变换矩阵的两列分别是基 (i^′,j^′)(\hat i', \hat j') 在基 (i^,j^)(\hat i, \hat j) 中的表示。

那反过来呢？如果已知基 (i^,j^)(\hat i, \hat j) 中的向量 a^′\hat a' 的表示，如何得到在基 (i^′,j^′)(\hat i', \hat j') 中的表示？

使用同样的方法。构建从基 (i^′,j^′)(\hat i', \hat j') 到 (i^,j^)(\hat i, \hat j) 变换矩阵。

i^=12i^′−12j^j^=12i^′+12j^′ \begin {aligned} \hat i &= \frac {1}{2} \hat i' - \frac {1}{2} \hat j \\ \hat j &= \frac {1}{2} \hat i' + \frac {1}{2} \hat j' \end {aligned}

则变换矩阵为：[1/21/2−1/21/2]\begin{bmatrix} 1/2 & 1/2 \\ -1/2 & 1/2 \end{bmatrix}，则：

[1/21/2−1/21/2][13]=[21] \begin{bmatrix} 1/2 & 1/2 \\ -1/2 & 1/2 \end{bmatrix} \begin{bmatrix} 1 \\ 3 \end{bmatrix} = \begin{bmatrix} 2 \\ 1 \end{bmatrix}

变换矩阵对任意向量都满足，进而可以推导出矩阵 [1/21/2−1/21/2]\begin{bmatrix} 1/2 & 1/2 \\ -1/2 & 1/2 \end{bmatrix} 和矩阵 [1−111]\begin{bmatrix}1 & -1 \\ 1 & 1\end{bmatrix} 互为逆矩阵。

也可以这样解释。定义基 (i^,j^)(\hat i, \hat j) 为 基 AA，基 (i^′,j^′)(\hat i', \hat j') 为基 BB，定义变换矩阵 [1−111]\begin{bmatrix}1 & -1 \\ 1 & 1\end{bmatrix} 为 AfromBA_{fromB}，定义变换矩阵 [1/21/2−1/21/2]\begin{bmatrix} 1/2 & 1/2 \\ -1/2 & 1/2 \end{bmatrix} 为 BfromAB_{fromA}。对于基 BB 中的任意向量 V^B\hat V_B，有：

AfromBV^B=V^ABfromAV^A=V^BBfromAAfromBV^B=V^BBfromAAfromB=E \begin{aligned} A_{fromB} \hat V_B &= \hat V_A \\ B_{fromA} \hat V_A &= \hat V_B \\ B_{fromA} A_{fromB} \hat V_B &= \hat V_B \\ B_{fromA} A_{fromB} &= E \end{aligned}

四、特征值和特征向量

对于某个变换 TT，变换前后方向相同或相反的向量 v^\hat v，称之为变换的特征向量；向量缩放的比例称之为特征值。根据方向不变，可得出：

Tv^=λv^ T \hat v = \lambda \hat v

根据上式，可得出：

(T−λI)v^=0 (T - \lambda I)\hat v = 0

从而推导出 det⁡(T−λI)=0\det(T-\lambda I) = 0，进而求得特征值 λ\lambda 的值。带入原公式，求得特征向量。值得注意的是，特征向量并不唯一，毕竟在同一个方向上的向量是无限的。

类似于上文提到的变换 [1−111]\begin{bmatrix}1 & -1 \\ 1 & 1\end{bmatrix}，因为改变了所有向量的方向，故而没有特征向量和特征值；类似于变换 [1101]\begin{bmatrix}1 & 1\\ 0 & 1\end{bmatrix}，X 轴上的所有向量的方向均没有发生改变，其他向量均有水平方向的拉伸，称之为切变，仅有一个大小为 1 特征值和一个方向的特征向量；而其他变换一般均有两个方向的特征向量。

举个例子🌰，变换 T=[0111]T = \begin{bmatrix}0 & 1 \\ 1 & 1\end{bmatrix}，根据公式可求得两个特征值为 1+52\frac {1 + \sqrt 5}{2} 和 1−52\frac {1 - \sqrt 5}{2}。进而取两个方向上的特征向量，这里选择 [21+5]\begin{bmatrix}2 \\ 1 + \sqrt 5\end{bmatrix} 和 [21−5]\begin{bmatrix}2 \\ 1 - \sqrt 5\end{bmatrix}。经过变换后，这两个方向上的向量只会发生缩放，缩放比例为特征值的大小，方向不会改变。

那么，如果以这两个向量为基呢？仍然令原基为基 AA，新基为 BB。易知：

AfromB=[221+51−5]BfromA=AfromB−1 \begin{aligned} A_{fromB} &= \begin{bmatrix}2 & 2\\ 1 + \sqrt 5 & 1 - \sqrt 5\end{bmatrix} \\ B_{fromA} &= A_{fromB}^{-1} \end{aligned}

可知在新基中，变换 TT 的表示为：

T′=BfromATAfromB=[1+52001−52] T' = B_{fromA} T A_{fromB} = \begin{bmatrix}\frac {1+\sqrt 5} {2} & 0 \\ 0 & \frac {1-\sqrt 5}{2}\end{bmatrix}

这是一个标准的对角矩阵。T′T' 为该变换在新基中的表示，也可以重新映射回原基中：

T=AfromBT′BfromA T = A_{fromB}T'B_{fromA}

最神奇的事情发生了。如果连续执行 nn 次 TT 变换，与在新基中连续执行 nn 次 T′T' 变换的效果是一致的：

Tn=AfromBT′nBfromA T^n = A_{fromB} T'{^n} B_{fromA}

而 T′T' 是对角矩阵，求 nn 次方即为求对角线上元素的 nn 次方。通过这种方式可以极大地降低计算复杂度。

仔细观察 TnT^n 的结果，可以手算一下 nn 较小时的值。实际上，TT 变换可以求 Fibonacci 数列，TnT^n 右上角的数即为 Fibonacci 数列的第 nn 项。使用特征值和特征向量，可以求得 Fibonacci 数列的通项公式。由：

Tn=[221+51−5][(1+52)n00(1−52)n][5−5205105+520−510] T^n = \begin{bmatrix}2 & 2\\ 1 + \sqrt 5 & 1 - \sqrt 5\end{bmatrix} \begin{bmatrix} (\frac {1+\sqrt 5} {2})^n & 0 \\ 0 & (\frac {1-\sqrt 5}{2})^n \end{bmatrix} \begin{bmatrix} \frac {5-\sqrt 5} {20} & \frac {\sqrt 5}{10} \\ \frac {5+\sqrt 5} {20} & -\frac {\sqrt 5}{10} \end{bmatrix}

可知：

Tn[0,1]=2(1+52)n510−2(1−52)n510=(1+52)n−(1−52)n5 \begin{aligned} T^n[0, 1] &= 2(\frac {1+\sqrt 5} {2})^n \frac {\sqrt 5} {10} - 2(\frac {1-\sqrt 5} {2})^n \frac {\sqrt 5} {10} \\ &= \frac {(\frac {1+\sqrt5} {2})^n - (\frac {1-\sqrt5} {2})^n} {\sqrt 5} \end{aligned}

五、奇异值分解

与特征值类似的，还有奇异值，对应的矩阵分解称之为奇异值分解（Singular Value Decomposition，SVD）：

M=UΣV∗ M = U\Sigma V^*

V∗V^*、Σ\Sigma 和 UU 的作用分别是旋转到 VV 的正交基、按照 Σ\Sigma 进行拉伸、旋转到 UU 的正交基，三个操作合成的效果与 MM 一致。VV 和 UU 分别是 M∗MM^*M 和 MM∗M M^* 的特征向量。Σ\Sigma 同样为对角矩阵，对角线上的数称为奇异值，从大到小排列，为 M∗MM^*M 和 MM∗M M^* 的特征值的非负平方根。

在维基百科上，有一个很清晰动画图示，点这里查看。

首先，需要理解清楚 UU 和 VV 的作用。对于一个单位正交基矩阵 VV，假设：

V=[acbd] V = \begin{bmatrix} a & c \\ b & d \end{bmatrix}

单位基意味着 a2+b2=1a^2 + b^2 = 1，c2+d2=1c^2 + d^2 = 1；正交意味着向量 [ab]\begin{bmatrix} a\\ b \end{bmatrix} 和 [cd]\begin{bmatrix} c\\ d \end{bmatrix} 垂直，即 ac+bd=0ac + bd = 0。比较神奇的是：

VTV=[abcd][acbd]=[1001] V^TV = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} a & c \\ b & d \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}

也就是说，VT=V−1V^T = V^{-1}。V∗V^* 称为 VV 的共轭矩阵，对于单位矩阵来说，V∗=V−1V^* = V^{-1}。定义原基为 AA，假设原基中的向量为 v^A\hat v_{A}，其在基 VV 下的表示为：

v^V=V∗v^A=V−1v^A=VTv^A \hat v_{V} = V^*\hat v_{A} = V^{-1} \hat v_{A} = V^T \hat v_{A}

在新基中，向量的长度并不会发生变化（可以自己推导一下），因此也可以认为只是进行了旋转操作。后面再通过对角矩阵 Σ\Sigma，向量在新基中实现了缩放。如果 Σ\Sigma 中对应的值为 0，则同时实现了投影。最后通过单位正交基矩阵 UU，再次完成一次旋转。

奇异值分解得到的三个矩阵，分别完成旋转、缩放和投影、旋转。另外，对于任意一个矩阵，都能完成奇异值分解，特征值就不一定了。网上也有关于奇异值和特征值的区别的讨论。

[待填坑]

参考文献

  1. 奇异值分解（We Recommend a Singular Value Decomposition），火光摇曳
  2. 奇异值分解，维基百科
Except where otherwise noted, content on this site is licensed under a CC BY-SA 4.0 license.
Copyright©2017 SF-Zhou, All Rights Reserved. Powered by GitHub Pages and GitHub Actions.